Going Back-to-Basics – Shrinkage: Solving Ridge and LASSO using Coordinate Descent from Scratch
Shrinkage methods: Ridge and LASSO
Ridge Regression
Ridge regression shrinks coefficients, \(\hat{\beta}\), by penalizing the residual sum of squares with a Lagrange multiplier, \(\lambda\).
\[\hat{\beta}^{ridge} = \operatorname*{arg\,min}_\beta \bigg\{ \sum_{i=1}^{N}\big(y_i - \beta_0 - \sum_{j=1}^{p} x_{ij}\beta_j\big)^2 +\lambda \sum_{j=1}^{p} \beta^2_j\bigg\}\]Written as the optimization,
\[\hat{\beta}^{ridge} = \operatorname*{arg\,min}_\beta \sum_{i=1}^{N}\big(y_i - \beta_0 - \sum_{j=1}^{p} x_{ij}\beta_j\big)^2,\\ \sum_{j=1}^{p} \beta^2_j\leq t\]for some \(t>0\). In matrix notation, the Lagrangian is written as,
\[L(X,t,\lambda^*,\beta ) =\|Y - X\beta\|_2^2 + \lambda^*(\|\beta\|_2^2 - t)\]where \(\|\bullet\|\) denotes the \(L_2\) norm. The optimal solution for the estimator, \(\hat{\beta}^{ridge}\), is proved with Karush-Kuhn-Tucker (KKT) conditions, \(\nabla_{\beta} L(X,c,\lambda^*,\beta ) = 0\) (stationarity) and \(\lambda^*(\|\beta(\lambda^*)\|_2^2 - t) = 0\) (Complementary slackness ). With the KKT conditions,
\[-2X^T(Y-X\beta) + 2t\beta = 0,\\ \lambda^*(\|\beta(\lambda^*)\|_2^2 - t) = 0\]Both conditions are satisfied if \(\lambda^* = \lambda\) and \(t = \lambda^*\|\beta(\lambda^*)\|_2^2\).
The solution to the ridge estimator is solved similar to linear regression.
\[RSS = (Y-\beta X)^T(Y-\beta X) - \lambda \beta^T \beta\]where the solution is
\[\hat{\beta}^{ridge} = (X^TX - \lambda I)^{-1} X^T Y\]LASSO Regression
Lasso regression is similar to ridge regression however \(L_2\) penalty is replaced by the \(L_1\) penalty.
\[\hat{\beta}^{ridge} = \operatorname*{arg\,min}_\beta \sum_{i=1}^{N}\big(y_i - \beta_0 - \sum_{j=1}^{p} x_{ij}\beta_j\big)^2,\\ \sum_{j=1}^{p} \mid\beta_j\mid \leq t\]Coordinated Decent is an efficient method for solving ridge and LASSO problems.
Coordinated Descent (Algorithim):
Coordinate descent is done by iteratively regressing a predictor, \(X_j\), on all currently explained predictors \(X_{-j}\). \(X\beta\) can be split into \(Y = X_j\beta_j + X_{-j}\beta_{-j}\).
\[Y = X_j\beta_j + X_{-j}\beta_{-j}\\ X_j \beta_j = y - x_{-j}\beta_{-j}\\ X_j^T X_j \beta_j = X_j^T (y - x_{-j}\beta_{-j})\\ \beta_j = \frac{X_j^T}{X_j^T X_j }(y - x_{-j}\beta_{-j})\]One cycle of coordinate descent iterates over each predictor. For a given set of parameters this is repeated. Typically, the algorithim is run for a value of \(\lambda\) such that \(\beta(\lambda_{max}) = 0\). This is repeated for a smaller value of \(\lambda\) using the previous of \(\lambda\) as a ‘warm-start’.
%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
import pandas as pd
import seaborn as sns
sns.set_context("notebook", font_scale=1.5, rc={"lines.linewidth": 1.5})
#for comparision
from sklearn import linear_model
from sklearn import datasets
import warnings
warnings.filterwarnings("ignore")
#testing with the prostate dataset
df = pd.read_csv('./prostate.data',sep='\s+')
df.head()
#split train and test
df_train = df.loc[df['train'] == 'T']
df_test = df.loc[df['train'] == 'F']
#drop train column
df_train = df_train.drop(['train'],axis=1)
df_test = df_test.drop(['train'],axis=1)
x_train = df_train[['lcavol', 'lweight', 'age', 'lbph', 'svi', 'lcp', 'gleason', 'pgg45']].to_numpy()
y_train = df_train[['lpsa']].to_numpy()
x_test = df_test[['lcavol', 'lweight', 'age', 'lbph', 'svi', 'lcp', 'gleason', 'pgg45']].to_numpy()
y_test = df_test[['lpsa']].to_numpy()
predictors = ['lcavol', 'lweight', 'age', 'lbph', 'svi', 'lcp', 'gleason', 'pgg45']
p = len(predictors)
cs = sns.color_palette("Set2", p)
#for ridge regression standardize the predictors
x_train = (x_train - np.mean(x_train,axis=0))/np.std(x_train,axis=0)
x_test = (x_test - np.mean(x_test,axis=0))/np.std(x_test,axis=0)
y_train = (y_train - np.mean(y_train,axis=0))/np.std(y_train,axis=0)
y_train = (y_train - np.mean(y_train,axis=0))/np.std(y_train,axis=0)
#Method Use Coordinate descent to solve for betas
import copy
beta = np.zeros((x_train.shape[1],1))
#Lasso coefficient/L1
def soft_threshold_l1(t : float,_lambda : float) -> float:
m = abs(t)
if t > 0 and m > _lambda:
return m - _lambda
elif t < 0 and m > _lambda:
return _lambda - m
else:
return 0.0
#Ridge coefficient/L2
def soft_threshold_l2(t : float ,_lambda : float) -> float:
return t / (1.0+_lambda)
#Coordinate descent
def coordinate_descent(lambda_range,x_train, y_train, beta, iterations=100, model = 'lasso'):
#Iterative Over Lambdas
#Start with beta(lambda_max) = 0
#then decrease to warm start the solution
for k,lval in enumerate(lambda_range):
#initalize r values
r = y_train - x_train @ beta
for i in range(iterations):
#iterate over predictors
for j in range(beta.shape[0]):
temp_beta = copy.deepcopy(beta)
temp_beta[j] = 0.0
r = y_train - x_train @ temp_beta
xtx = np.sum(x_train[:,j]**2)
betaj = (1/xtx) * (x_train[:,j].T @ r)
if model == 'lasso':
beta[j] = soft_threshold_l1(betaj[0],lval)
elif model == 'ridge':
beta[j] = soft_threshold_l2(betaj[0],lval)
lambda_sol[k] = beta.T
return lambda_sol
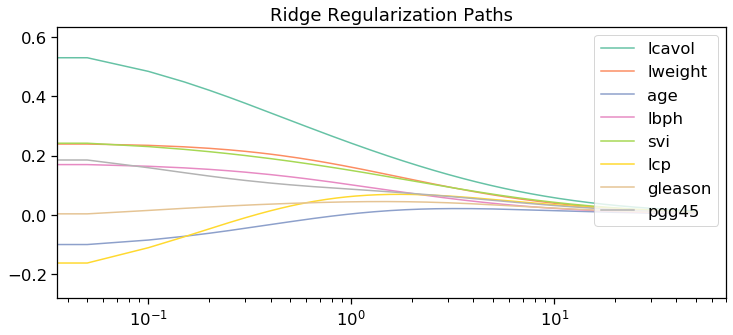
#Ridge Solutions
lambda_tot = 1000
lambda_sol = np.zeros((lambda_tot,beta.shape[0]))
lambda_range = np.arange(0,50,50.0/lambda_tot)[::-1]
lambda_sol = coordinate_descent(lambda_range, x_train, y_train, beta, model = 'ridge')
m,n = x_train.shape
#Solution via coordinate_descent method
fig, ax = plt.subplots(1,1,figsize=(12,5))
x = lambda_range
ax.set_title("L2/Ridge Regularization Path")
for i in range(n):
ax.semilogx(x, lambda_sol[:,i],color=cs[i],label=predictors[i])
ax.set_title('Ridge Regularization Paths')
ax.legend(loc='upper right')
plt.axis('tight')
(0.035399060013482114,
70.55272086458793,
-0.28090154214315,
0.6347657236127785)
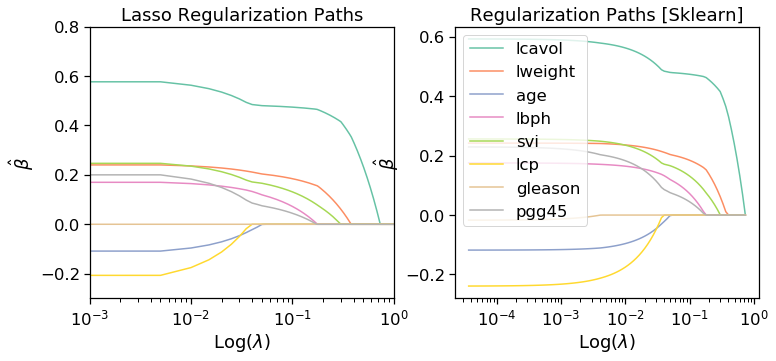
#Lasso Solutions
lambda_tot = 200
lambda_sol = np.zeros((lambda_tot,beta.shape[0]))
lambda_range = np.arange(0,1,1.0/lambda_tot)[::-1]
lambda_sol = coordinate_descent(lambda_range, x_train, y_train, beta, model = 'lasso')
m,n = x_train.shape
#Solution via coordinate_descent method
fig, ax = plt.subplots(1,2,figsize=(12,5))
x = lambda_range
ax[0].set_title("L1/LASSO Regularization Path")
for i in range(n):
ax[0].semilogx(x, lambda_sol[:,i],color=cs[i],label=predictors[i])
#sklearn validation
alphas_lasso, coefs_lasso, _ = linear_model.lasso_path(x_train, y_train,\
5e-5 , fit_intercept=False)
for i in range(n):
ax[1].semilogx(alphas_lasso, coefs_lasso[0][i],\
label = predictors[i], color=cs[i])
for a in ax:
a.set_xlim((0.001,1))
a.set_ylim((-0.3,0.8))
a.set_xlabel(r"Log($\lambda$)")
a.set_ylabel(r"$\hat{\beta}$")
ax[0].set_title('Lasso Regularization Paths')
ax[1].set_title('Regularization Paths [Sklearn]')
ax[1].legend()
plt.axis('tight')
(2.2341606180573485e-05,
1.2029494762168695,
-0.28064122726898855,
0.6346202023890164)